Harmonic Formation
By Richard Merrick
How do harmonics form?
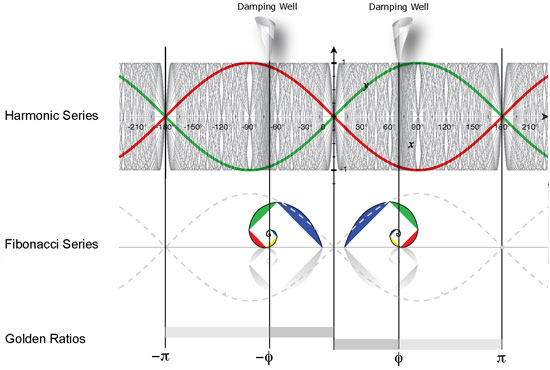
As waves reflect and resonate inside a container or cavity, they cross one another. As they cross, they exchange energy at specific locations called ‘damping wells.’ In quantum mechanics this is explained by Landau-Zener theory (1932).
Known as Landau damping, waves that pass through one another mostly transparently, avoiding a direct collision, are called ‘avoided crossings.’ In such cases, energy is exchanged in a ‘parameter zone’ where one wave pushes against another, creating a kind of spinning well or vortex action. Like a kind of switch, energy is passed ‘adiabatically’ (without heat loss) across the damping well in a kind of torque action.
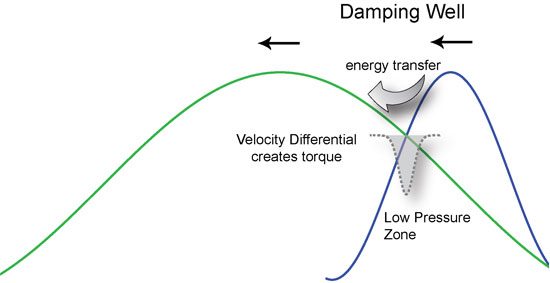
We can think of the damping well as a kind of low-pressure zone much like those in our atmosphere that create storms, hurricanes and tornados. The surrounding pressure differential causes an implosion toward the center of the low-pressure zone, forming a vortex.
In the special case of a standing wave, damping wells form at constant locations at golden sections of the period of the prime resonant frequency. This is because the golden ratio constant, represented by the Greek letter _ (or Phi) and equal to the ratio of about 1 : 0.618033… or 1.618033, is non-reflective while having the unique ability to nest into itself infinitely. As a result, energy is exchanged between harmonics at Phi proportions while harmonic wave partials begin to ripple outward from the edge of the well.
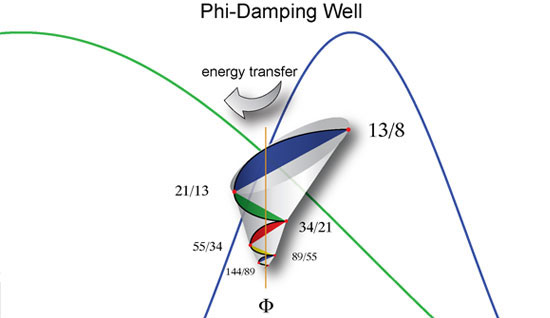
Because of this, the damping well of a standing waves can be described as a Fibonacci spiral converging to Phi, the deadest location in a standing wave and thus the point of greatest torque and energy exchange between harmonics. This can be proven by using the Fibonacci series as a nominal solution for the second-order equation known as the ‘characteristic wave damping equation.’ In this proof, the golden ratio Phi becomes the ‘eigenvector’ and the Fibonacci series (1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …} become its ‘eigenvalues.’
In fact, we can understand harmonic formation as something called ‘phi-heterodyning’ where each harmonic emerges around the Phi eigenvector in nested golden sections like a fractal. A paper by Bovenkamp and Giandinoto entitled ‘Incorporation of the Golden Ratio Phi into the Schrödinger Wave Function using the Phi Recursive Heterodyning Set’ shows how this can occur, but there is an easier way to visualize it.
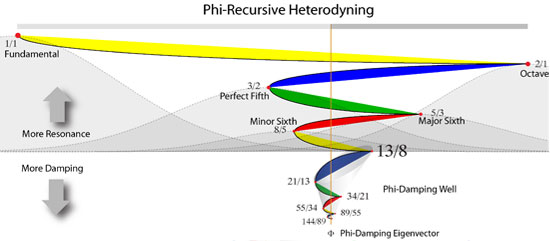
The Fibonacci damping well approximates the irrational Phi Recursive Heterodyning Set with rational harmonic waves. Above the proportion of 13:8, wave formation is damped and suppressed while below this in the range of {1 .. 12} whole number harmonics can form and resonate constructively with the prime resonant frequency. In general, waves that come too close to Phi proportions in the resonant frequency are killed while those furthest away resonate the most.
While this sounds like a new idea, it is actually part of the age-old practice of creating resonant chambers that suppress the formation of unwanted standing waves and reflection. Stradivarius was well-known for using golden sections in the design of his violins. The best rectangular concert halls use golden proportions in their dimensions, as do modern day speaker enclosures.
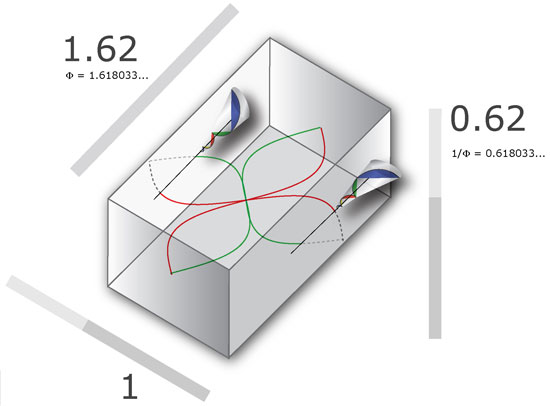
Standing wave reflection simply cannot be sustained when one of the three dimensions in a container is at or even near a golden ratio to another.
Content courtesy of Richard Merrick
Copyright (c) 2011. All Rights Reserved.