Quantum electrodynamics is a field of physics that studies the interaction of electromagnetic radiation with electrically charged matter within the framework of relativity and quantum mechanics. More plainly put, it is a relativistic quantum field theory of electromagnetism. It basically describes how light and matter interact. More specifically it deals with the interactions between electrons, positrons and photons.
It is the fundamental theory underlying all disciplines of science concerned with electromagnetism, such as atomic physics, chemistry, biology, the theory of bulk matter, and electromagnetic radiation.
It has been called “the jewel of physics” for its extremely accurate predictions of quantities like the anomalous magnetic moment of the electron, and the Lamb shift of the energy levels of hydrogen.
It is the first physical theory ever developed that has no obvious intrinsic limitation and describes physical quantities from first principles. Nature accommodates forces other than the electromagnetic force, such as those responsible for radioactive disintegration of heavy nuclei (called the weak force) and the force that binds the nucleus together (called the strong force). A theory called the standard model, has been developed which unifies the three forces and accounts for all experimental data from very low to extremely high energies. This does not mean, however, that quantum electrodynamics fails at high energies. It simply means that the real world has forces other than electromagnetism.
The History of Quantum Electrodynamics
The word ‘quantum’ is Latin, meaning “how much” (neut. sing. of quantus “how great”). The word ‘electrodynamics’ was coined by André-Marie Ampère in 1822. The word ‘quantum’, as used in physics, i.e. with reference to the notion of count, was first used by Max Planck, in 1900 and reinforced by Einstein in 1905 with his use of the term light quanta.
Quantum theory began in 1900, when Max Planck assumed that energy is quantized in order to derive a formula predicting the observed frequency dependence of the energy emitted by a black body. This dependence is completely at variance with classical physics. In 1905, Einstein explained the photoelectric effect by postulating that light energy comes in quanta later called photons. In 1913, Bohr invoked quantization in his proposed explanation of the spectral lines of the hydrogen atom. In 1924, Louis de Broglie proposed a quantum theory of the wave-like nature of subatomic particles. The phrase “quantum physics” was first employed in Johnston’s Planck’s Universe in Light of Modern Physics. These theories, while they fit the experimental facts to some extent, were strictly phenomenological: they provided no rigorous justification for the quantization they employed.
Modern quantum mechanics was born in 1925 with Werner Heisenberg’s matrix mechanics and Erwin Schrödinger’s wave mechanics and the Schrödinger equation, which was a non-relativistic generalization of de Broglie’s(1925) relativistic approach. Schrödinger subsequently showed that these two approaches were equivalent. In 1927, Heisenberg formulated his uncertainty principle, and the Copenhagen interpretation of quantum mechanics began to take shape. Around this time, Paul Dirac, in work culminating in his 1930 monograph finally joined quantum mechanics and special relativity, pioneered the use of operator theory, and devised the bra-ket notation widely used since. In 1932, John von Neumann formulated the rigorous mathematical basis for quantum mechanics as the theory of linear operators on Hilbert spaces. This and other work from the founding period remains valid and widely used.
Quantum chemistry began with Walter Heitler and Fritz London’s 1927 quantum account of the covalent bond of the hydrogen molecule. Linus Pauling and others contributed to the subsequent development of quantum chemistry.
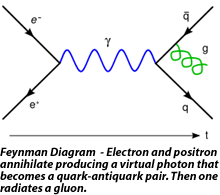
The application of quantum mechanics to fields rather than single particles, resulting in what are known as quantum field theories, began in 1927. Early contributors included Dirac, Wolfgang Pauli, Weisskopf, and Jordan. This line of research culminated in the 1940s in the quantum electrodynamics (QED) of Richard Feynman, Freeman Dyson, Julian Schwinger, and Sin-Itiro Tomonaga, for which Feynman, Schwinger and Tomonaga received the 1965 Nobel Prize in Physics. QED, a quantum theory of electrons, positrons, and the electromagnetic field, was the first satisfactory quantum description of a physical field and of the creation and annihilation of quantum particles.
QED involves a covariant and gauge invariant prescription for the calculation of observable quantities. Feynman’s mathematical technique, based on his diagrams, initially seemed very different from the field-theoretic, operator-based approach of Schwinger and Tomonaga, but Freeman Dyson later showed that the two approaches were equivalent. The renormalization procedure for eliminating the awkward infinite predictions of quantum field theory was first implemented in QED. Even though renormalization works very well in practice, Feynman was never entirely comfortable with its mathematical validity, even referring to renormalization as a “shell game” and “hocus pocus”. (Feynman, 1985: 128)
QED has served as the model and template for all subsequent quantum field theories. One such subsequent theory is quantum chromodynamics, which began in the early 1960s and attained its present form in the 1975 work by H. David Politzer, Sidney Coleman, David Gross and Frank Wilczek. Building on the pioneering work of Schwinger, Peter Higgs, Goldstone, and others, Sheldon Glashow, Steven Weinberg and Abdus Salam independently showed how the weak nuclear force and quantum electrodynamics could be merged into a single electroweak force.
References:
Wikipedia –Â History of Quantum Electrodynamics
