Fibonacci numbers are a sequence of numbers named after the medieval mathematician Leonardo Pisano, known as Fibonacci (1157-1250). Fibonacci numbers and the Fibonacci sequence are prime examples of ‘how mathematics is connected to seemingly unrelated things.’ All of the great architecture of the past can be defined and explained using this simple series of numbers, which also defines the Golden Section or Divine Proportion used in the great buildings of the golden era of architecture starting with the great pyramid at Giza in Egypt.
These numbers were discussed in 1202 in Fibonacci’s book ‘Liber Abaci,’ where it introduced the sequence to Western European mathematics, although the sequence had been previously described in Indian mathematics. The discovery of this series of numbers is probably one of the most significant events in the history of mathematics and its direct bearing on the relationship between music and sacred geometry, that is the foundation for an incredible mathematical relationship behind phi. They continue to remain fascinating and mysterious to people today.
The first number of the sequence is 0, the second number is 1, and each subsequent number is equal to the sum of the previous two numbers of the sequence itself, yielding the sequence 0, 1, 1, 2, 3, 5, 8, etc.
e.g. 1+2 = 3 2+3 = 5 3+5 = 8 thus giving us the following sequence:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811…
In mathematical terms, it is defined by the following recurrence relation:
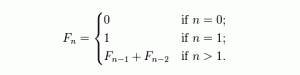
The ratio of each successive pair of numbers in the series approximates phi (1.618. . .) as 5 divided by 3 is 1.666…, and 8 divided by 5 is 1.60.
After the 40th number in the series, the ratio is accurate to 15 decimal places. How did this come about? At this time in the 12th century, mathematical competitions and challenges were quite common. In 1225 Fibonacci took part in a tournament at Pisa ordered by Frederick II, the Holy Roman Emperor.
One of the problems set to the competitors was: Beginning with a single pair of rabbits, if every month each productive pair bears a new pair, which becomes productive when they are 1 month old, how many rabbits will there be after n months?
The short answer is that, as a result of solving this problem, Fibonacci gave us the Fibonacci series of numbers which have served us well to this day!
FIBONACCI SPIRALS IN NATURE
Uses of the Fibonacci Number System and the Golden Ratio span nature architecture, and art.
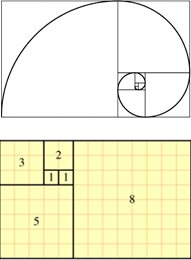The Fibonacci numbers are Nature’s numbering system. They appear everywhere in Nature, from the leaf arrangement in plants, to the pattern of the florets of a flower, the bracts of a pine cone, or the scales of a pineapple. The Fibonacci numbers are therefore applicable to the growth of every living thing, including a single cell, a grain of wheat, a hive of bees, and even all of mankind.
