The Golden Ratio
The golden ratio, also known as the golden proportion, golden mean, golden section, golden number, and divine proportion is the division of a given unit of length into two parts such that the ratio of the shorter to the longer equals the ratio of the longer part to the whole or, when a line is divided such that the ratio of the longer part of the line to the whole is exactly the same ratio as the shorter part of the line is to the longer part.
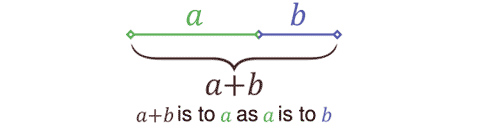
It is a number often encountered when taking the ratios of distances in simple geometric figures, such as the pentagon, pentagram, decagon and dodecahedron. It is a ratio or proportion defined by the number Phi = 1.618033988749895… It is an irrational number, meaning it is a number that cannot be written as a simple fraction – the decimal goes on forever without repeating. Phi, like Pi, is a ratio defined by a geometric construction.
Just as Pi is the ratio of the circumference of a circle to its diameter, Phi is simply the ratio of the line segments that result when a line is divided in one very special and unique way.
The figure of a golden section illustrates the geometric relationship that defines this constant. Expressed algebraically:
![]()
This equation has as its unique positive solution the algebraic irrational number:
![]()
Shapes proportioned according to the golden ratio have long been considered aesthetically pleasing throughout many cultures, and is still used frequently in art and design, suggesting a natural balance between symmetry and asymmetry.
The ancient Pythagoreans, who defined numbers as expressions of ratios (and not as units as is common today), believed that reality is numerical and that the golden ratio expressed an underlying truth about existence.
The Golden Ratio seems to get its name from the Golden Rectangle, a rectangle whose sides are in the proportion of the Golden Ratio.
The theory of the Golden Rectangle is an aesthetic one, that the ratio is an aesthetically pleasing one and so can be found spontaneously or deliberately turning up in a great deal of art. The front of the Parthenon can be comfortably framed with a Golden Rectangle. Additional classic subdivisions of the rectangle align perfectly with major architectural features of the structure.

The Golden Rectangle can be used to create a spiral, the Golden Spiral. Starting with one Golden Rectangle, a second Golden Rectangle can be attached to the first using the longest side of the rectangle, side A as the shortest side B of the next rectangle. To this end the second rectangle is constructed 90 degrees perpendicular to the first rectangle. If this process is continued, called the spiraling of the Golden Rectangle, a curved line can be drawn through the corners of the rectangles creating the Golden Mean spiral. The spiraling of the Golden Mean spiral continues indefinitely in inward and outward directions, it’s getting smaller and smaller spiraling inwards and getting bigger and bigger spiraling outwards.
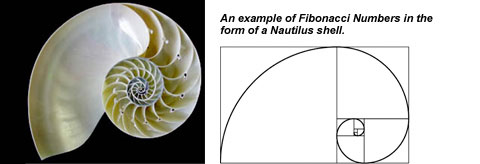
Another connection of the Golden Ratio to partial symmetries in nature is through the Fibonacci Numbers. This is a number series where each member is simply the sum of the previous two numbers. Fibonacci spirals and Golden Mean ratios appear everywhere in the universe. The spiral is the natural flow form of water when it is going down the drain. It is also the natural flow form of air in tornadoes and hurricanes. Here’s another beautiful example of a Fibonacci spiral in nature, it’s the Nautilus shell and every book about sacred geometry contains one:
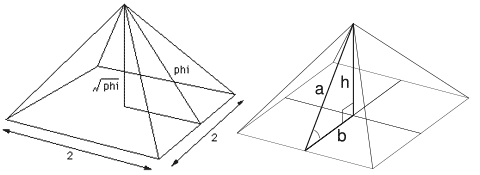
The Great Pyramid of Giza’s dimensions are also based on the Golden Ratio. If we take a cross section of the Great Pyramid, we get a right triangle, the so-called Egyptian Triangle. The ratio of the slant height of the pyramid (hypotenuse of the triangle) to the distance from ground center (half the base dimension) is 1.61804 … which differs from phi by only one unit in the fifth decimal place. If we let the base dimension be 2 units, then the sides of the right triangle are in the proportion 1:sqrt(phi):phi and the pyramid has a height of sqrt(phi).
Leonardo Da Vinci exhibited the golden ratio in many of his paintings and illustrations calling it the De Divina Proportione or ‘divine proportion’. He conducted an entire exploration of the human body and the ratios of the lengths of various body parts.